Løse likninger numerisk

Teori

Ofte kan vi komme borti likninger som er vanskelige å løse for hånd. Da kan vi ta i bruk en metode for å løse likningen numerisk. Dette gir oss en tilnærmet tallverdi for svaret.

Alle likninger kan enkelt skrives med $0$ på høyre side. Dette er du vant med å gjøre når du løser andregradslikninger.

$x^2 = 8x-6$

$x^2 -8x + 6 = 0$

Å løse likningen er nå det samme som å finne nullpunkt til funksjonen $f(x)=x^2-3x+6$. For å gjøre det bruker vi:

Halveringsmetoden for å løse likninger

1. Skriv om likningen som en funksjon $f(x)= 0$
2. Velg to verdier $a$ og $b$ slik at $f(a)$ og $f(b)$ har motsatte fortegn. (Da må funksjonen være null et sted i mellom)
3. Finn midtpunktet mellom $a$ og $b$: $c=\dfrac{a+b}{2}$
4. Sjekk om $f(x)\approx0$. Hvis ikke, fortsett til punkt 5.
5. Sjekk fortegnet til $f(c)$. Dersom $f(a)$ og $f(c)$ har samme fortegn, la $c$ bli den nye verdien til $a$. Hvis ikke, la $c$ bli den nye verdien til $b$.
6. Gå til punkt 3.

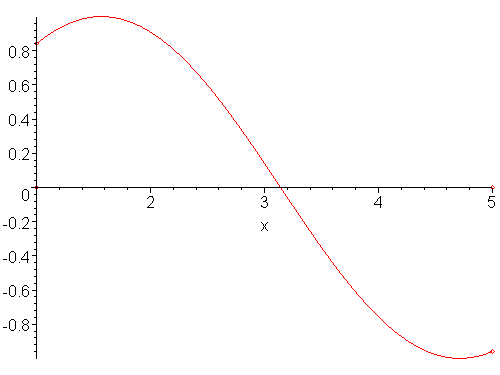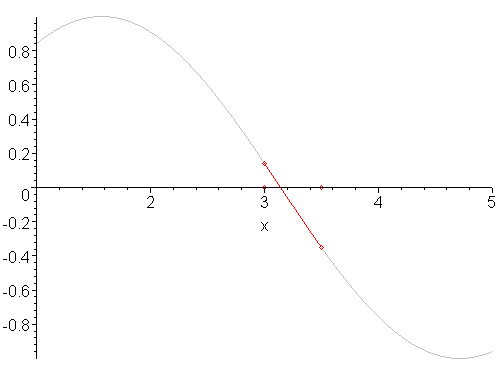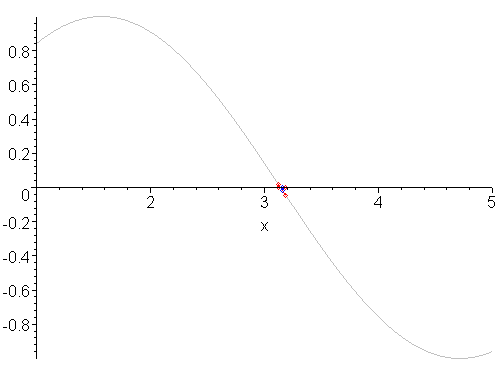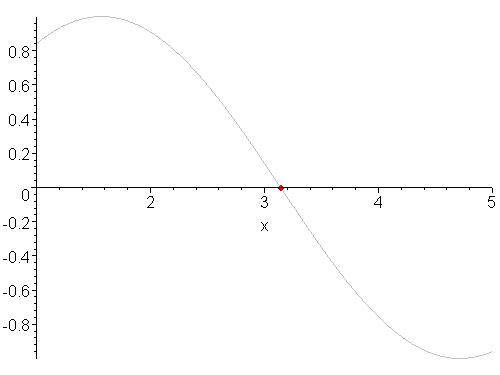(Animasjonen viser en annen funksjon)

def f(x):
    return x**2-8*x+6

def halvering(f, a, b):
    antall = 0
    c = 0
    while abs(f(c)) > 1e-4 and antall < 100:
        c = (a+b) / 2
        if f(a)*f(c) > 0:       # produktet av to tall er positiv bare dersom de har samme fortegn
            a = c
        else:
            b = c
        antall += 1
    return c, antall

nullpunkt, antall = halvering(f, 0, 4)    # starter med a=0 og b=4
print(f"Funksjonen har nullpunkt i x={nullpunkt:.5f}. Brukte {antall} steg.")

Funksjonen har nullpunkt i x=0.83771. Brukte 16 steg.

Oppgaver

1. Finn en ekkel likning i matteboka di (eller et annet sted). Løs den med halveringsmetoden.
2. Det er litt tungvint å måtte velge verdier for a og b selv. Lag en ny funksjon halvering2(f) som selv leter etter a og b før den bruker halveringsmetoden.
3. (Vanskelig) Har du lært Newtons metode i matematikk? Lag en funksjon newton(f, x0) som finner nullpunktet til f (med x0 som startverdi) ved hjelp av Newtons metode. Du kan se i boka på s. 188 for hjelp.